Mengenal Lebih Dalam Bangun Datar: Jenis, Sifat, dan Rumusnya

2025-02-20 edukasi by admin
Mengenal Lebih Dalam Bangun Datar: Jenis, Sifat, dan Rumusnya

Oke, siap! Berikut adalah konten artikel tentang bangun datar yang dioptimalkan untuk SEO, dengan memperhatikan semua instruksi yang Anda berikan:

Preview: Mari selami dunia bangun datar, dari kotak hingga lingkaran, dan pelajari semua yang perlu Anda ketahui tentangnya. Panduan lengkap ini akan membahas jenis-jenis, sifat-sifat, rumus, dan contoh penggunaannya dalam kehidupan sehari-hari.

Apa Itu Bangun Datar? Pengertian dan Definisi

Bangun datar adalah objek dua dimensi yang memiliki panjang dan lebar, tetapi tidak memiliki tinggi. Mereka hanya dapat diukur dalam dua dimensi. Pemahaman tentang bangun datar sangat penting dalam matematika dan berbagai aplikasi praktis lainnya.

Jenis-Jenis Bangun Datar yang Perlu Anda Ketahui

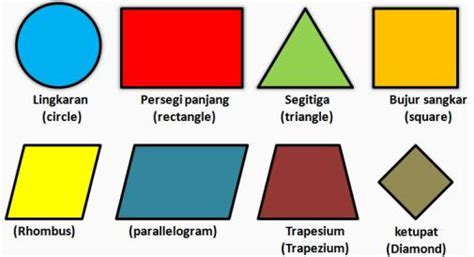
Ada banyak jenis bangun datar yang berbeda, masing-masing dengan sifat dan karakteristik unik. Berikut beberapa jenis yang paling umum:

    1. Persegi: Bangun datar dengan empat sisi yang sama panjang dan empat sudut siku-siku (90 derajat).

    2. Persegi Panjang: Bangun datar dengan empat sisi, di mana sisi-sisi yang berhadapan sama panjang dan semua sudutnya siku-siku.

    3. Segitiga: Bangun datar dengan tiga sisi dan tiga sudut. Ada berbagai jenis segitiga, termasuk segitiga sama sisi, segitiga sama kaki, dan segitiga siku-siku.

    4. Lingkaran: Bangun datar yang terdiri dari semua titik yang berjarak sama dari titik pusat.

    5. Trapesium: Bangun datar dengan empat sisi, di mana setidaknya dua sisi sejajar.

    6. Jajar Genjang: Bangun datar dengan empat sisi yang berpasangan sejajar. Sisi-sisi yang berhadapan sama panjang, dan sudut-sudut yang berhadapan sama besar.

    7. Belah Ketupat: Bangun datar dengan empat sisi yang sama panjang. Sisi-sisi yang berhadapan sejajar, dan sudut-sudut yang berhadapan sama besar.

      8. Sifat-Sifat Penting Bangun Datar

      Setiap jenis bangun datar memiliki sifat-sifat khusus yang membedakannya dari yang lain. Beberapa sifat penting meliputi:

    8. Jumlah Sisi: Jumlah sisi yang membentuk bangun datar.

    9. Jumlah Sudut: Jumlah sudut yang ada di dalam bangun datar.

    10. Panjang Sisi: Ukuran panjang sisi-sisi bangun datar.

    11. Besar Sudut: Ukuran sudut-sudut di dalam bangun datar.

    12. Simetri: Apakah bangun datar memiliki simetri (garis yang membagi bangun datar menjadi dua bagian yang identik).

      13. Rumus-Rumus Dasar Bangun Datar

      Untuk menghitung luas dan keliling bangun datar, kita menggunakan rumus-rumus khusus. Berikut beberapa rumus dasar:

    13. Persegi:

      14. * Luas = Sisi x Sisi

      * Keliling = 4 x Sisi

    14. Persegi Panjang:

      15. * Luas = Panjang x Lebar

      * Keliling = 2 x (Panjang + Lebar)

    15. Segitiga:

      16. * Luas = 1/2 x Alas x Tinggi

      * Keliling = Jumlah semua sisi

    16. Lingkaran:

      17. * Luas = π x r² (π = pi, r = jari-jari)

      * Keliling (Lingkar) = 2 x π x r

      Contoh Penggunaan Bangun Datar dalam Kehidupan Sehari-hari

      Bangun datar ada di sekitar kita! Perhatikan contoh-contoh ini:

    17. Persegi: Ubin lantai, papan catur, bingkai foto.

    18. Persegi Panjang: Pintu, jendela, layar televisi.

    19. Segitiga: Atap rumah, rambu lalu lintas.

    20. Lingkaran: Roda, jam dinding, pizza.

      21. Mengapa Mempelajari Bangun Datar Penting?

      Memahami konsep bangun datar sangat penting karena:

    21. Dasar Matematika: Membentuk dasar untuk konsep geometri yang lebih kompleks.

    22. Pemecahan Masalah: Membantu dalam memecahkan masalah praktis yang melibatkan pengukuran dan perhitungan luas dan keliling.

    23. Aplikasi Sehari-hari: Digunakan dalam arsitektur, desain interior, teknik, dan banyak bidang lainnya.

      24. Pertanyaan Umum (FAQ) Seputar Bangun Datar

    24. Apa itu bangun datar?

      25. Bangun datar adalah bangun datar dua dimensi yang hanya memiliki panjang dan lebar.

    25. Sebutkan contoh bangun datar!

      26. Contoh bangun datar termasuk persegi, persegi panjang, segitiga, lingkaran, dan trapesium.

    26. Apa perbedaan antara persegi dan persegi panjang?

      27. Persegi memiliki empat sisi yang sama panjang dan empat sudut siku-siku, sedangkan persegi panjang memiliki sisi-sisi yang berhadapan sama panjang dan empat sudut siku-siku.

    27. Bagaimana cara menghitung luas lingkaran?

      28. Luas lingkaran dihitung menggunakan rumus πr², di mana π (pi) adalah konstanta matematika sekitar 3.14, dan r adalah jari-jari lingkaran.

    28. Apa pentingnya mempelajari bangun datar?

Mempelajari bangun datar penting karena merupakan dasar untuk konsep geometri yang lebih kompleks, membantu dalam pemecahan masalah praktis, dan digunakan dalam berbagai bidang seperti arsitektur dan desain.

Kesimpulan

Pemahaman tentang bangun datar adalah fondasi penting dalam matematika dan memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Dengan memahami jenis-jenis, sifat-sifat, dan rumus-rumusnya, Anda dapat mengembangkan kemampuan pemecahan masalah dan mengaplikasikannya dalam berbagai situasi.

Related Post