Memahami Kuartil: Contoh Soal dan Pembahasan Lengkap
Baik, berikut adalah konten artikel yang dioptimalkan SEO sesuai dengan instruksi yang Anda berikan:
Kuartil adalah salah satu konsep penting dalam statistika yang membantu kita membagi data menjadi empat bagian yang sama. Artikel ini akan membahas secara mendalam tentang contoh soal kuartil, lengkap dengan pembahasan yang mudah dipahami. Siap belajar? Yuk, simak selengkapnya!
Apa itu Kuartil? (Pengertian dan Jenis)
Sebelum kita membahas contoh soal kuartil, mari kita pahami dulu apa itu kuartil dan jenis-jenisnya. Kuartil adalah nilai-nilai yang membagi data yang telah diurutkan menjadi empat bagian yang sama besar. Ada tiga jenis kuartil:
- Kuartil Bawah (Q1): Nilai yang memisahkan 25% data terendah dari sisanya.
- Kuartil Tengah (Q2): Nilai tengah data, sama dengan median.
- Kuartil Atas (Q3): Nilai yang memisahkan 25% data tertinggi dari sisanya.
- Data sudah terurut.
- Jumlah data (n) = 9.
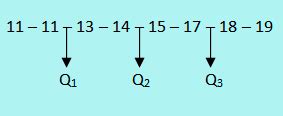
- Q2 (Median) = Nilai tengah = 9
- Q1 = Nilai tengah dari data sebelum Q2, yaitu 3, 5, 7, 8. Jadi, Q1 = (5+7)/2 = 6
- Q3 = Nilai tengah dari data setelah Q2, yaitu 11, 13, 15, 17. Jadi, Q3 = (13+15)/2 = 14
- Data sudah terurut.
- Jumlah data (n) = 6.
- Q2 (Median) = (6+8)/2 = 7
- Q1 = Nilai tengah dari data sebelum Q2, yaitu 2, 4, 6. Jadi, Q1 = 4
- Q3 = Nilai tengah dari data setelah Q2, yaitu 8, 10, 12. Jadi, Q3 = 10
- Menentukan Letak Kuartil:
- Menghitung Kuartil:
- Urutkan Data: Pastikan data sudah terurut dari terkecil hingga terbesar.
- Pahami Rumus: Hafalkan rumus untuk data tunggal dan data kelompok.
- Teliti: Periksa kembali perhitungan Anda untuk menghindari kesalahan.
Dengan memahami konsep kuartil, kita dapat lebih mudah menganalisis dan menginterpretasikan data.
Contoh Soal Kuartil Data Tunggal
Mari kita mulai dengan beberapa contoh soal kuartil untuk data tunggal. Ini adalah dasar yang penting sebelum kita membahas data kelompok yang lebih kompleks.
Contoh Soal 1:
Tentukan kuartil bawah (Q1), kuartil tengah (Q2), dan kuartil atas (Q3) dari data berikut: 3, 5, 7, 8, 9, 11, 13, 15, 17.
Pembahasan:
Contoh Soal 2:
Tentukan kuartil bawah (Q1), kuartil tengah (Q2), dan kuartil atas (Q3) dari data berikut: 2, 4, 6, 8, 10, 12.
Pembahasan:
Contoh Soal Kuartil Data Kelompok
Sekarang, mari kita beralih ke contoh soal kuartil untuk data kelompok. Ini melibatkan sedikit perhitungan yang lebih kompleks.
Contoh Soal 3:
Berikut adalah tabel distribusi frekuensi berat badan siswa:
| Berat Badan (kg) | Frekuensi |
|---|---|
| 40-44 | 4 |
| 45-49 | 6 |
| 50-54 | 10 |
| 55-59 | 8 |
| 60-64 | 2 |
Tentukan kuartil bawah (Q1), kuartil tengah (Q2), dan kuartil atas (Q3).
Pembahasan:
* Jumlah frekuensi (n) = 30
Letak Q1 = 1/4 n = 1/4 * 30 = 7.5 (berada di kelas interval 45-49)
Letak Q2 = 1/2 n = 1/2 * 30 = 15 (berada di kelas interval 50-54)
Letak Q3 = 3/4 n = 3/4 * 30 = 22.5 (berada di kelas interval 55-59)
Rumus umum: Qi = Tb + [(i/4 n - fkum) / fi ] p
Dimana:
* Tb = Tepi Bawah kelas kuartil
* i = Kuartil ke - i (1,2,3)
* n = Jumlah Frekuensi
* fkum = Frekuensi kumulatif sebelum kelas kuartil
* fi = Frekuensi kelas kuartil
* p = Panjang interval kelas
Q1 = 44.5 + [(7.5 - 4)/6] 5 = 44.5 + (3.5/6)*5 = 44.5 + 2.92 = 47.42
Q2 = 49.5 + [(15 - 10)/10] 5 = 49.5 + (5/10)*5 = 49.5 + 2.5 = 52
Q3 = 54.5 + [(22.5 - 20)/8] 5 = 54.5 + (2.5/8)*5 = 54.5 + 1.56 = 56.06
Tips dan Trik Menghitung Kuartil
Berikut beberapa tips untuk mempermudah perhitungan kuartil:
Tanya Jawab Seputar Kuartil
T: Apa perbedaan kuartil dengan desil?
J: Kuartil membagi data menjadi empat bagian, sedangkan desil membagi data menjadi sepuluh bagian.
T: Mengapa kita perlu menghitung kuartil?
J: Kuartil membantu kita memahami distribusi data dan mengidentifikasi nilai-nilai penting seperti nilai tengah dan penyebaran data.
T: Bagaimana jika jumlah data ganjil saat menghitung kuartil data tunggal?
J: Median adalah nilai tengah. Q1 adalah nilai tengah dari data yang lebih rendah dari median. Q3 adalah nilai tengah dari data yang lebih tinggi dari median.
Semoga dengan penjelasan dan contoh soal kuartil di atas, Anda semakin memahami konsep ini. Selamat belajar!