Menguasai Vektor: Kumpulan Contoh Soal Vektor Lengkap dengan Pembahasan

2025-02-17 Edukasi by admin

Oke, siap! Berikut adalah konten artikel yang dioptimalkan berdasarkan instruksi yang Anda berikan:

`markdown

Vektor adalah konsep fundamental dalam fisika dan matematika. Memahami vektor dengan baik sangat penting untuk menguasai materi-materi lanjutan. Artikel ini akan membahas berbagai contoh soal vektor beserta penyelesaiannya, sehingga kamu bisa lebih memahami konsep vektor dan meningkatkan kemampuan menyelesaikan soal. Yuk, simak!

Mengapa Contoh Soal Vektor Penting?

Memahami teori vektor saja tidak cukup. Kamu perlu berlatih menyelesaikan contoh soal vektor untuk benar-benar menguasai konsep ini. Dengan mengerjakan soal, kamu akan terbiasa mengaplikasikan rumus-rumus vektor dalam berbagai situasi. Selain itu, contoh soal vektor juga membantu kamu mengidentifikasi area-area yang masih perlu kamu pelajari lebih dalam.

Jenis-Jenis Soal Vektor dan Pembahasannya

Berikut adalah beberapa jenis contoh soal vektor yang sering muncul, lengkap dengan pembahasannya:

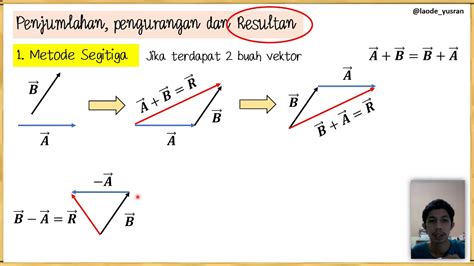
1. Penjumlahan dan Pengurangan Vektor

Contoh Soal:

Diberikan dua vektor: a = 3i + 2j dan b = -i + 5j. Tentukan vektor c = a + b.

Pembahasan:

Untuk menjumlahkan vektor, cukup jumlahkan komponen-komponen yang sesuai:

c = a + b = (3i + 2j) + (-i + 5j) = (3 - 1)i + (2 + 5)j = 2i + 7j

2. Perkalian Vektor dengan Skalar

Contoh Soal:

Diberikan vektor v = 4i - 3j. Tentukan vektor w = 2v.

Pembahasan:

Untuk mengalikan vektor dengan skalar, kalikan setiap komponen vektor dengan skalar tersebut:

w = 2v = 2(4i - 3j) = (2 4)i - (2 3)j = 8i - 6j

3. Perkalian Titik (Dot Product)

Contoh Soal:

Diberikan vektor p = 2i + 3j dan q = i - j. Tentukan p. q.

Pembahasan:

Perkalian titik dihitung dengan menjumlahkan hasil perkalian komponen-komponen yang sesuai:

p. q = (2 1) + (3 -1) = 2 - 3 = -1

4. Perkalian Silang (Cross Product)

Contoh Soal:

Diberikan vektor r = i + j + k dan s = 2i - j + k. Tentukan r x s.

Pembahasan:

Perkalian silang dihitung menggunakan determinan matriks:

r x s = | i j k |

| 1 1 1 |

| 2 -1 1 |

r x s = (1 1 - 1 -1)i - (1 1 - 1 2)j + (1 -1 - 1 2)k = 2i + j - 3k

5. Mencari Sudut Antara Dua Vektor

Contoh Soal:

Diberikan vektor u = 3i + 4j dan v = 5i - 12j. Tentukan sudut antara u dan v.

Pembahasan:

Gunakan rumus: cos θ = (u. v) / (|u| * |v|)

u. v = (3 5) + (4 * -12) = 15 - 48 = -33

|u| = √(3² + 4²) = √25 = 5

|v| = √(5² + (-12)²) = √169 = 13

cos θ = -33 / (5 * 13) = -33 / 65

θ = arccos(-33/65) ≈ 119.5°

Tips dan Trik dalam Menyelesaikan Soal Vektor

Visualisasikan Vektor: Gambarlah vektor jika memungkinkan. Ini akan membantu kamu memahami arah dan besarnya vektor.

Perhatikan Satuan: Pastikan semua vektor menggunakan satuan yang sama.

Pahami Rumus: Hafalkan rumus-rumus dasar vektor seperti penjumlahan, pengurangan, perkalian titik, dan perkalian silang.

Latihan: Semakin banyak kamu berlatih menyelesaikan contoh soal vektor, semakin mahir kamu dalam menguasai konsep ini.

Tautan Internal

Untuk pemahaman lebih lanjut, kamu bisa membaca artikel kami tentang [link artikel tentang dasar-dasar vektor].

Tanya Jawab Seputar Vektor

Q: Apa perbedaan perkalian titik dan perkalian silang?

A: Perkalian titik (dot product) menghasilkan skalar, sedangkan perkalian silang (cross product) menghasilkan vektor yang tegak lurus terhadap kedua vektor awal.

Q: Bagaimana cara menentukan arah vektor hasil perkalian silang?

A: Gunakan kaidah tangan kanan. Arahkan jari-jari tangan kananmu searah vektor pertama, tekuk jari-jarimu searah vektor kedua, maka ibu jarimu akan menunjukkan arah vektor hasil perkalian silang.

Q: Kapan kita menggunakan perkalian titik dan kapan menggunakan perkalian silang?

A: Perkalian titik digunakan untuk mencari proyeksi satu vektor ke vektor lain atau untuk menentukan sudut antara dua vektor. Perkalian silang digunakan untuk mencari vektor yang tegak lurus terhadap dua vektor lain, atau untuk menghitung momen gaya.

Semoga artikel ini bermanfaat! Teruslah berlatih contoh soal vektor agar kamu semakin mahir!

Penjelasan:

Meta Description: Ditempatkan di awal, ringkas dan mengandung kata kunci utama.

Judul: Singkat dan jelas, mengandung kata kunci utama.

Paragraf Pertama: Memperkenalkan topik dan menekankan pentingnya contoh soal vektor.

Sub Judul (H2): Menggunakan kata kunci dan variasinya.

Contoh Soal: Memberikan berbagai tipe soal vektor dan pembahasannya yang detail.

Tips dan Trik: Meningkatkan nilai artikel bagi pembaca.

Tautan Internal: Menghubungkan ke artikel terkait. (Pastikan untuk mengganti "[link artikel tentang dasar-dasar vektor]" dengan tautan yang sesuai).