Menguasai Rumus Volume Tabung: Panduan Lengkap dan Mudah Dipahami

2025-02-16 Edukasi by admin
Menguasai Rumus Volume Tabung: Panduan Lengkap dan Mudah Dipahami

Baik, berikut adalah konten artikel yang dioptimalkan dengan parameter yang Anda berikan:

Preview: Apakah Anda kesulitan menghitung volume tabung? Artikel ini akan memandu Anda langkah demi langkah, mulai dari definisi hingga contoh soal, agar Anda menguasai rumus volume tabung dengan mudah.

Memahami Dasar: Apa Itu Tabung dan Mengapa Volume Penting?

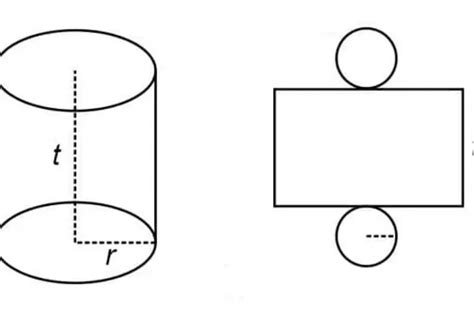
Tabung adalah bangun ruang tiga dimensi yang dibentuk oleh dua lingkaran identik yang sejajar dan sebuah persegi panjang yang melengkung di antara kedua lingkaran tersebut. Konsep volume sangat penting karena memungkinkan kita menghitung kapasitas suatu tabung, yang berguna dalam berbagai aplikasi sehari-hari, mulai dari menghitung volume air dalam pipa hingga merancang kaleng minuman.

Rumus Volume Tabung: Kunci untuk Menghitung Kapasitas

Inti dari menghitung volume tabung terletak pada rumus volume tabung itu sendiri. Rumusnya sangat sederhana:

Volume Tabung = π r² t

Dimana:

    1. π (pi) adalah konstanta matematika yang kira-kira bernilai 3.14 atau 22/7.

    2. r adalah jari-jari alas tabung (lingkaran).

    3. t adalah tinggi tabung.

      4. Memecah Rumus: Memahami Setiap Komponen

    4. π (Pi): Konstanta ini selalu sama, jadi Anda tidak perlu menghitungnya. Ingat saja nilainya, yaitu sekitar 3.14 atau 22/7.

    5. r² (Jari-jari Kuadrat): Jari-jari adalah jarak dari pusat lingkaran ke tepi lingkaran. Kuadratkan jari-jari (kalikan jari-jari dengan dirinya sendiri) untuk mendapatkan luas alas lingkaran.

    6. t (Tinggi): Tinggi adalah jarak antara kedua alas lingkaran pada tabung.

      7. Langkah-Langkah Menghitung Volume Tabung dengan Mudah

      Berikut adalah langkah-langkah sederhana untuk menghitung volume tabung:

    7. Ukur Jari-Jari (r): Ukur jari-jari alas lingkaran tabung. Jika Anda hanya mengetahui diameter (jarak dari satu sisi lingkaran ke sisi lain melalui pusat), bagi diameter dengan 2 untuk mendapatkan jari-jari.

    8. Ukur Tinggi (t): Ukur tinggi tabung.

    9. Hitung Luas Alas (π * r²): Kalikan π dengan kuadrat jari-jari.

    10. Hitung Volume (Luas Alas * Tinggi): Kalikan luas alas dengan tinggi tabung.

      11. Contoh Soal: Mempraktikkan Rumus Volume Tabung

      Soal 1: Sebuah tabung memiliki jari-jari 5 cm dan tinggi 10 cm. Berapakah volumenya?

      Penyelesaian:

    11. r = 5 cm

    12. t = 10 cm

      13. Volume = π r² t = 3.14 (5 cm)² 10 cm = 3.14 25 cm² * 10 cm = 785 cm³

      Soal 2: Sebuah kaleng susu berbentuk tabung memiliki diameter 8 cm dan tinggi 15 cm. Berapakah volumenya?

      Penyelesaian:

    13. Diameter = 8 cm, maka r = Diameter / 2 = 4 cm

    14. t = 15 cm

      15. Volume = π r² t = 3.14 (4 cm)² 15 cm = 3.14 16 cm² * 15 cm = 753.6 cm³

      Tips dan Trik: Memudahkan Perhitungan Volume Tabung

    15. Perhatikan Satuan: Pastikan semua satuan (jari-jari, tinggi, dan volume) konsisten. Jika jari-jari dalam cm dan tinggi dalam meter, ubah salah satunya terlebih dahulu.

    16. Gunakan Kalkulator: Gunakan kalkulator untuk mempermudah perhitungan, terutama saat mengkuadratkan jari-jari atau mengalikan dengan π.

    17. Pahami Konsep: Memahami konsep dasar volume tabung akan membantu Anda memecahkan soal-soal yang lebih kompleks.

      18. Aplikasi Rumus Volume Tabung dalam Kehidupan Sehari-hari

      Rumus volume tabung tidak hanya berguna dalam pelajaran matematika. Aplikasi praktisnya sangat luas, termasuk:

    18. Teknik Sipil: Menghitung volume air yang dapat ditampung dalam pipa atau tangki air.

    19. Arsitektur: Merancang bangunan dengan mempertimbangkan kapasitas ruang berbentuk tabung, seperti silo atau tangki penyimpanan.

    20. Industri Makanan dan Minuman: Menentukan ukuran kemasan produk berbentuk tabung, seperti kaleng atau botol.

    21. Manufaktur: Merancang komponen mesin berbentuk tabung, seperti silinder.

Tanya Jawab (FAQ)

Q: Apa itu jari-jari dalam rumus volume tabung?

A: Jari-jari adalah jarak dari pusat lingkaran alas tabung ke tepi lingkaran tersebut. Anda juga bisa mendapatkan jari-jari dengan membagi diameter (garis lurus yang melewati pusat lingkaran) dengan 2.

Q: Kapan saya harus menggunakan 3.14 atau 22/7 untuk π?

A: Gunakan 22/7 jika jari-jari atau tinggi tabung merupakan kelipatan 7, karena akan memudahkan perhitungan. Jika tidak, gunakan 3.14 untuk hasil yang lebih akurat.

Q: Bagaimana jika tabung tidak memiliki alas yang berbentuk lingkaran sempurna?

A: Rumus volume tabung yang kita bahas di sini hanya berlaku untuk tabung dengan alas lingkaran sempurna. Jika alasnya berbentuk elips atau bentuk lainnya, Anda perlu menggunakan rumus yang berbeda.

Kesimpulan

Memahami dan menguasai rumus volume tabung sangat penting untuk berbagai aplikasi praktis. Dengan mengikuti panduan langkah demi langkah dan berlatih dengan contoh soal, Anda akan dapat menghitung volume tabung dengan mudah dan akurat. Jangan ragu untuk kembali ke artikel ini jika Anda membutuhkan referensi di masa depan.

Related Post