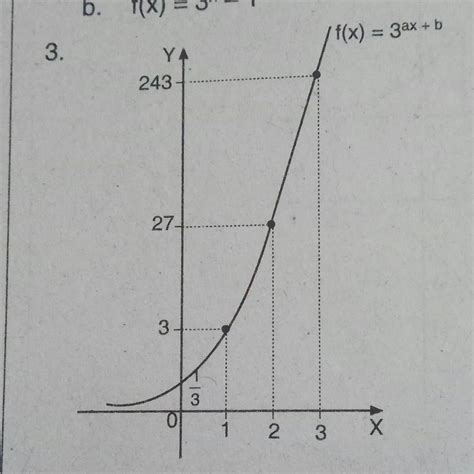
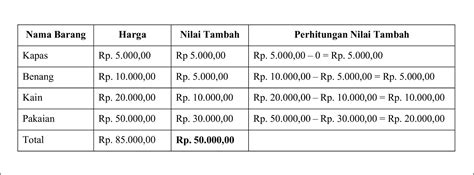
Menguasai Pertidaksamaan Linear Dua Variabel: Contoh Soal dan Pembahasan Lengkap

Baik, berikut adalah konten artikel yang dioptimalkan berdasarkan instruksi yang Anda berikan:
`markdown
Bingung dengan pertidaksamaan linear dua variabel? Jangan khawatir! Artikel ini akan membantumu memahaminya dengan tuntas melalui berbagai contoh soal pertidaksamaan linear dua variabel beserta pembahasannya yang jelas dan mudah dimengerti. Mari kita mulai!
Apa Itu Pertidaksamaan Linear Dua Variabel?
Sebelum masuk ke contoh soal pertidaksamaan linear dua variabel, mari kita pahami dulu definisinya. Pertidaksamaan linear dua variabel adalah kalimat matematika yang memiliki dua variabel (biasanya x dan y) dan dihubungkan dengan tanda pertidaksamaan seperti < (kurang dari), > (lebih dari), ≤ (kurang dari atau sama dengan), atau ≥ (lebih dari atau sama dengan).
Bentuk umum pertidaksamaan linear dua variabel adalah:
ax + by < c*
ax + by > c*
ax + by ≤ c*
ax + by ≥ c*
di mana a, b, dan c adalah konstanta, dan x dan y adalah variabel.
Mengapa Mempelajari Pertidaksamaan Linear Dua Variabel Penting?
Pertidaksamaan linear dua variabel sering digunakan untuk memodelkan situasi dunia nyata yang melibatkan batasan atau kendala. Contohnya, menentukan kombinasi jumlah barang yang dapat dibeli dengan anggaran tertentu atau menentukan wilayah yang memenuhi syarat untuk mendapatkan subsidi. Memahami konsep ini sangat penting untuk berbagai aplikasi praktis dalam matematika, ekonomi, dan bidang lainnya.
Contoh Soal Pertidaksamaan Linear Dua Variabel dan Pembahasannya
Berikut adalah beberapa contoh soal pertidaksamaan linear dua variabel yang sering muncul dan bagaimana cara menyelesaikannya:
Contoh Soal 1:
Tentukan daerah penyelesaian dari pertidaksamaan 2x + y ≤ 6.
Pembahasan:
- Ubah pertidaksamaan menjadi persamaan: 2x + y = 6
- Gambar garis: Cari dua titik yang memenuhi persamaan tersebut. Misalnya, jika x = 0, maka y = 6. Titik (0, 6). Jika y = 0, maka x = 3. Titik (3, 0). Hubungkan kedua titik ini untuk mendapatkan garis.
- Uji titik: Pilih titik di luar garis (misalnya, titik (0, 0)) dan substitusikan ke dalam pertidaksamaan awal: 2(0) + 0 ≤ 6 => 0 ≤ 6. Pernyataan ini benar.
- Arsir daerah: Karena titik (0, 0) memenuhi pertidaksamaan, maka daerah yang mengandung titik (0, 0) adalah daerah penyelesaiannya. Arsir daerah di bawah garis 2x + y = 6. Karena tanda pertidaksamaan adalah "≤", maka garisnya digambar solid (bukan putus-putus).
- Gambar setiap garis: Lakukan seperti pada contoh soal 1 untuk setiap pertidaksamaan, mengubahnya menjadi persamaan dan mencari titik potong.
- Uji titik: Uji titik (0, 0) untuk setiap pertidaksamaan.
- Arsir daerah: Arsir daerah yang memenuhi semua pertidaksamaan. Daerah penyelesaian adalah daerah yang tumpang tindih dari semua arsiran. Karena x ≥ 0 dan y ≥ 0, maka daerah penyelesaian berada di kuadran I.
- Pahami konsep dasar: Pastikan Anda memahami perbedaan antara pertidaksamaan dan persamaan.
- Gunakan grafik: Grafik sangat membantu memvisualisasikan daerah penyelesaian.
- Latihan soal: Semakin banyak Anda berlatih, semakin terampil Anda dalam menyelesaikan soal.
- Perhatikan tanda pertidaksamaan: Tanda pertidaksamaan menentukan arah arsiran dan apakah garisnya solid atau putus-putus.
- Meta Description: Ditempatkan di awal dan mengandung kata kunci utama.
- Judul (H1): Singkat, menarik, dan mengandung kata kunci.
- Deskripsi Awal Paragraf: Mengandung kata kunci dan menjelaskan isi artikel secara singkat.
- H2 dan Terstruktur, relevan, dan mengandung kata kunci.
- Contoh Soal: Diberikan dengan pembahasan yang jelas dan langkah-langkah yang mudah diikuti.
- Tips dan Trik: Memberikan nilai tambah bagi pembaca.
- FAQ: Menjawab pertanyaan umum terkait topik.
- Penggunaan Kata Kunci: Kata kunci utama dan variasinya digunakan secara alami di seluruh artikel.
- Teks Bold, Italic, dan Strong: Digunakan untuk menyoroti kata kunci dan poin-poin penting.
- Gaya Penulisan: Informatif dan mudah dipahami.
- Tautan Internal: (Meskipun tidak ada di sini, Anda bisa menambahkan tautan ke artikel lain yang relevan di blog Anda).
Contoh Soal 2:
Tentukan daerah penyelesaian dari sistem pertidaksamaan berikut:
x + y ≥ 4*
2x + y ≤ 8*
x ≥ 0*
y ≥ 0*
Pembahasan:
Contoh Soal 3: Soal Cerita
Seorang pedagang buah memiliki modal Rp 1.000.000. Ia ingin membeli apel dan jeruk. Harga apel Rp 4.000 per kg dan harga jeruk Rp 2.000 per kg. Jika pedagang tersebut hanya dapat memuat 400 kg buah, buatlah model matematika dari permasalahan tersebut.
Pembahasan:
Misalkan:
x* = jumlah apel (kg)
y* = jumlah jeruk (kg)
Maka, model matematikanya adalah:
4000x + 2000y ≤ 1000000 (modal) => 2x + y ≤ 500* (disederhanakan)
x + y ≤ 400* (kapasitas muatan)
x ≥ 0*
y ≥ 0*
Tips dan Trik Mengerjakan Soal Pertidaksamaan Linear Dua Variabel
Kesimpulan
Memahami pertidaksamaan linear dua variabel sangat penting untuk berbagai aplikasi matematika dan kehidupan sehari-hari. Dengan memahami konsep dasar, berlatih contoh soal pertidaksamaan linear dua variabel, dan mengikuti tips di atas, Anda akan mampu menguasai materi ini dengan mudah.
Tanya Jawab (FAQ)
T: Apa perbedaan antara pertidaksamaan linear satu variabel dan dua variabel?
J: Pertidaksamaan linear satu variabel hanya memiliki satu variabel (misalnya, x), sedangkan pertidaksamaan linear dua variabel memiliki dua variabel (misalnya, x dan y).
T: Bagaimana cara menentukan apakah suatu titik merupakan penyelesaian dari pertidaksamaan linear dua variabel?
J: Substitusikan koordinat titik tersebut ke dalam pertidaksamaan. Jika pertidaksamaan tersebut benar, maka titik tersebut merupakan penyelesaian.
T: Apa arti garis putus-putus pada grafik pertidaksamaan linear dua variabel?
J: Garis putus-putus menunjukkan bahwa titik-titik pada garis tersebut tidak termasuk dalam daerah penyelesaian. Ini terjadi jika tanda pertidaksamaan adalah < atau >.
T: Mengapa x dan y selalu lebih besar atau sama dengan nol (x ≥ 0 dan y ≥ 0) dalam soal cerita yang melibatkan kuantitas?
J: Karena kuantitas (seperti jumlah barang) tidak mungkin bernilai negatif.
`
Penjelasan:
Semoga artikel ini bermanfaat!