Menguasai Luas Permukaan Tabung: Contoh Soal dan Pembahasan Lengkap
Oke, siap! Berikut adalah konten artikel yang dioptimalkan berdasarkan panduan yang Anda berikan:
Preview: Bingung bagaimana cara menghitung luas permukaan tabung? Artikel ini akan membahas secara detail konsep luas permukaan tabung beserta contoh soal dan pembahasannya yang mudah dipahami. Siap untuk meningkatkan kemampuan matematikamu? Mari kita mulai!
Memahami Konsep Luas Permukaan Tabung
Tabung adalah bangun ruang tiga dimensi yang memiliki alas dan tutup berbentuk lingkaran yang identik, serta selimut berbentuk persegi panjang yang menghubungkan kedua lingkaran tersebut. Menghitung luas permukaan tabung penting dalam berbagai aplikasi praktis, mulai dari menghitung kebutuhan bahan untuk membuat kaleng hingga menghitung volume tangki penyimpanan.
Secara sederhana, luas permukaan tabung adalah total luas seluruh permukaan yang menyusun tabung tersebut. Ini terdiri dari:
- Dua buah lingkaran (alas dan tutup)
- Satu buah selimut (permukaan tegak yang menghubungkan alas dan tutup)
- π (pi) ≈ 3.14 atau 22/7
- r = jari-jari lingkaran alas/tutup
- t = tinggi tabung
- Diketahui:
- Rumus:
- Penyelesaian:
- Diketahui:
- Rumus:
- Penyelesaian:
- Diketahui:
- Rumus:
- Penyelesaian:
- Pahami Rumus: Pastikan Anda hafal rumus luas permukaan tabung dan mengerti arti setiap variabel.
- Perhatikan Satuan: Pastikan semua satuan yang digunakan konsisten (misalnya, semuanya dalam cm atau meter).
- Gambar Sketsa: Menggambar sketsa tabung dapat membantu Anda memvisualisasikan soal dan memahami informasi yang diberikan.
- Latihan Soal: Semakin banyak Anda mengerjakan contoh soal luas permukaan tabung, semakin terampil Anda dalam menyelesaikan soal-soal sejenis.
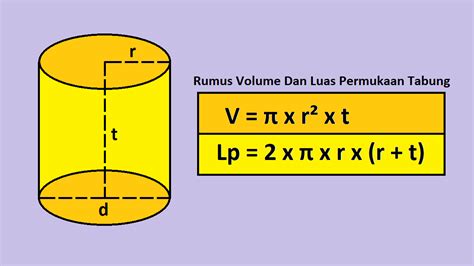
Rumus untuk menghitung luas permukaan tabung adalah:
Luas Permukaan = 2πr (r + t)
Dimana:
Contoh Soal Luas Permukaan Tabung dan Pembahasannya
Berikut adalah beberapa contoh soal luas permukaan tabung beserta pembahasannya yang akan membantu Anda memahami konsep ini lebih dalam.
Contoh Soal 1: Menghitung Luas Permukaan Dasar
Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah luas permukaan tabung tersebut!
Pembahasan:
* r = 7 cm
* t = 10 cm
Luas Permukaan = 2πr (r + t)
Luas Permukaan = 2 (22/7) 7 * (7 + 10)
Luas Permukaan = 44 * 17
Luas Permukaan = 748 cm²
Jadi, luas permukaan tabung tersebut adalah 748 cm².
Contoh Soal 2: Mencari Tinggi Tabung
Sebuah tabung memiliki luas permukaan 528 cm² dan jari-jari alas 4 cm. Tentukan tinggi tabung tersebut!
Pembahasan:
* Luas Permukaan = 528 cm²
* r = 4 cm
Luas Permukaan = 2πr (r + t)
528 = 2 (22/7) 4 * (4 + t)
528 = (176/7) * (4 + t)
(528 * 7) / 176 = 4 + t
21 = 4 + t
t = 21 - 4
t = 17 cm
Jadi, tinggi tabung tersebut adalah 17 cm.
Contoh Soal 3: Aplikasi dalam Kehidupan Sehari-hari
Sebuah kaleng berbentuk tabung akan dicat seluruh permukaannya. Jika jari-jari alas kaleng 5 cm dan tingginya 12 cm, berapa luas permukaan yang harus dicat?
Pembahasan:
Soal ini adalah aplikasi langsung dari konsep luas permukaan tabung. Anda hanya perlu menggunakan rumus seperti contoh sebelumnya untuk mendapatkan jawabannya.
* r = 5 cm
* t = 12 cm
Luas Permukaan = 2πr (r + t)
Luas Permukaan = 2 3.14 5 * (5 + 12)
Luas Permukaan = 10 3.14 17
Luas Permukaan = 533.8 cm²
Jadi, luas permukaan kaleng yang harus dicat adalah 533.8 cm².
Tips dan Trik Mengerjakan Soal Luas Permukaan Tabung
Tanya Jawab Seputar Luas Permukaan Tabung
Q: Mengapa kita perlu menghitung luas permukaan tabung?
A: Menghitung luas permukaan tabung berguna dalam banyak aplikasi praktis, seperti menghitung jumlah bahan yang dibutuhkan untuk membuat suatu benda berbentuk tabung (misalnya, kaleng), menghitung luas permukaan yang perlu dicat, atau menghitung perpindahan panas pada benda berbentuk tabung.
Q: Apakah π (pi) selalu 3.14?
A: Nilai π (pi) adalah angka irasional yang memiliki desimal tak terhingga. Namun, untuk perhitungan praktis, kita sering menggunakan aproksimasi 3.14 atau 22/7. Penggunaan 22/7 biasanya lebih akurat jika jari-jari atau tinggi tabung merupakan kelipatan 7.
Q: Apa perbedaan antara luas permukaan tabung dan volume tabung?
A: Luas permukaan tabung adalah total luas seluruh permukaan tabung, sedangkan volume tabung adalah ruang yang ditempati oleh tabung tersebut. Keduanya memiliki rumus yang berbeda dan mengukur hal yang berbeda. Volume tabung dihitung dengan rumus πr²t.
Kesimpulan
Memahami konsep luas permukaan tabung adalah keterampilan matematika yang penting dan berguna. Dengan memahami rumus dan berlatih contoh soal luas permukaan tabung, Anda akan semakin mahir dalam menyelesaikan soal-soal yang berkaitan dengan topik ini. Jangan ragu untuk terus berlatih dan mencari sumber belajar lainnya untuk memperdalam pemahaman Anda.
Semoga artikel ini bermanfaat! Saya sudah berusaha memasukkan semua instruksi dan optimasi yang Anda berikan.