Menguasai Contoh Soal Identitas Trigonometri: Panduan Lengkap dan Pembahasan
Oke, siap! Berikut adalah konten artikel yang dioptimalkan berdasarkan instruksi yang Anda berikan:
`markdown
Identitas trigonometri adalah pondasi penting dalam memahami matematika lebih lanjut, khususnya kalkulus dan fisika. Penting untuk memahami dan mengaplikasikan identitas trigonometri dengan baik agar sukses dalam mata pelajaran tersebut. Artikel ini akan membahas secara mendalam contoh soal identitas trigonometri beserta solusi lengkapnya, membantu Anda memahami konsepnya dan siap menghadapi berbagai variasi soal.
Apa Itu Identitas Trigonometri?
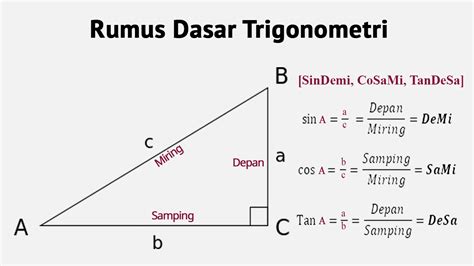
Identitas trigonometri adalah persamaan yang selalu benar untuk semua nilai variabel (sudut) di mana fungsi trigonometri tersebut terdefinisi. Identitas ini memungkinkan kita untuk menyederhanakan ekspresi trigonometri yang rumit menjadi bentuk yang lebih sederhana dan mudah dikerjakan. Beberapa identitas dasar yang perlu Anda ketahui adalah:
- sin² θ + cos² θ = 1
- tan θ = sin θ / cos θ
- cot θ = cos θ / sin θ
- sec θ = 1 / cos θ
- csc θ = 1 / sin θ
- Ingat identitas dasar: sin² θ + cos² θ = 1, maka 1 - cos² θ = sin² θ
- Substitusikan: (sin² θ) / sin θ
- Sederhanakan: sin θ
- Ekspansikan kuadrat: (sin² x + 2 sin x cos x + cos² x) + (sin² x - 2 sin x cos x + cos² x)
- Sederhanakan: sin² x + cos² x + sin² x + cos² x (perhatikan bahwa 2 sin x cos x saling menghilangkan)
- Gunakan identitas dasar sin² x + cos² x = 1: 1 + 1
- Hasil akhir: 2
- Ubah tan θ dan cot θ ke sin θ dan cos θ: (sin θ / cos θ) + (cos θ / sin θ)
- Samakan penyebut: (sin² θ + cos² θ) / (sin θ cos θ)
- Gunakan identitas dasar sin² θ + cos² θ = 1: 1 / (sin θ cos θ)
- Pisahkan pecahan: (1 / sin θ) * (1 / cos θ)
- Ubah ke sec θ dan csc θ: csc θ * sec θ
- Gunakan identitas dasar: sin² A + cos² A = 1
- Substitusikan nilai sin A: (3/5)² + cos² A = 1
- Selesaikan untuk cos² A: cos² A = 1 - (9/25) = 16/25
- Cari cos A: cos A = √(16/25) = 4/5 (karena A sudut lancip, cos A positif)
- Hitung tan A: tan A = sin A / cos A = (3/5) / (4/5) = 3/4
- Kuasai Identitas Dasar: Hafalkan dan pahami identitas dasar trigonometri. Ini adalah kunci untuk menyelesaikan berbagai soal.
- Ubah Semua Fungsi ke Sin dan Cos: Jika Anda bingung, ubah semua fungsi trigonometri ke sin dan cos. Ini seringkali mempermudah penyelesaian.
- Lihat Tujuan Akhir: Perhatikan identitas yang ingin dibuktikan atau ekspresi yang ingin disederhanakan. Ini akan membantu Anda menentukan langkah yang tepat.
- Latihan Soal: Semakin banyak Anda berlatih, semakin terbiasa Anda dengan berbagai jenis soal dan cara penyelesaiannya.
Contoh Soal Identitas Trigonometri dan Pembahasan
Berikut adalah beberapa contoh soal identitas trigonometri yang sering muncul, dilengkapi dengan langkah-langkah penyelesaiannya:
Soal 1: Buktikan identitas berikut: (1 - cos² θ) / sin θ = sin θ
Pembahasan:
Terbukti bahwa (1 - cos² θ) / sin θ = sin θ
Soal 2: Sederhanakan ekspresi berikut: (sin x + cos x)² + (sin x - cos x)²
Pembahasan:
Jadi, (sin x + cos x)² + (sin x - cos x)² = 2
Soal 3: Buktikan identitas berikut: tan θ + cot θ = sec θ csc θ
Pembahasan:
Terbukti bahwa tan θ + cot θ = sec θ csc θ
Soal 4: Jika sin A = 3/5 dan A adalah sudut lancip, tentukan nilai dari cos A dan tan A.
Pembahasan:
Jadi, cos A = 4/5 dan tan A = 3/4
Tips dan Trik Mengerjakan Soal Identitas Trigonometri
Tanya Jawab (FAQ) tentang Identitas Trigonometri
T: Apa pentingnya mempelajari identitas trigonometri?
J: Identitas trigonometri sangat penting dalam berbagai bidang, seperti matematika (kalkulus, geometri), fisika (gerak harmonik, optik), dan teknik (elektronika, telekomunikasi). Memahami identitas trigonometri akan mempermudah penyelesaian masalah dalam bidang-bidang tersebut.
T: Bagaimana cara menghafal identitas trigonometri dengan mudah?
J: Cobalah menggunakan jembatan keledai atau mnemonic untuk menghafal identitas dasar. Selain itu, dengan sering mengerjakan contoh soal identitas trigonometri, Anda akan secara otomatis menghafal identitas tersebut.
T: Apakah ada aplikasi atau website yang bisa membantu saya belajar identitas trigonometri?
J: Ya, banyak aplikasi dan website yang menyediakan materi pembelajaran, latihan soal, dan kalkulator trigonometri. Beberapa contohnya adalah Wolfram Alpha, Khan Academy, dan Symbolab.
T: Apa yang harus saya lakukan jika saya kesulitan menyelesaikan soal identitas trigonometri?
J: Jangan menyerah! Coba kembali melihat identitas dasar dan contoh soal yang sudah dibahas. Jika masih kesulitan, cari bantuan dari guru, teman, atau sumber belajar online. Ingatlah, latihan secara teratur adalah kunci keberhasilan.
Kesimpulan
Memahami dan mengaplikasikan contoh soal identitas trigonometri sangat penting untuk keberhasilan Anda dalam matematika dan bidang terkait. Dengan menguasai identitas dasar, menerapkan strategi yang tepat, dan berlatih secara teratur, Anda akan mampu menyelesaikan berbagai variasi soal identitas trigonometri dengan mudah. Selamat belajar!
`