Memahami Rumus Tabung: Volume, Luas Permukaan, dan Contoh Soal

2025-02-19 edukasi by admin

Oke, siap! Berikut adalah draf artikel tentang rumus tabung, dioptimalkan untuk SEO, dan ditulis dengan bahasa Indonesia yang baik dan benar:

`markdown

(Preview Konten) Tabung adalah bangun ruang yang sering kita temui sehari-hari, mulai dari kaleng minuman hingga pipa air. Artikel ini akan membahas tuntas rumus tabung, mulai dari cara menghitung volume, luas permukaan, hingga contoh soal dan pembahasannya. Mari kita pelajari bersama!

Apa Itu Tabung?

Tabung adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Bagian-bagian penting dari tabung adalah:

Jari-jari (r): Jarak dari pusat lingkaran ke tepi lingkaran.

Tinggi (t): Jarak antara dua lingkaran sejajar.

Rumus Tabung: Panduan Lengkap

1. Rumus Volume Tabung

Volume tabung adalah ruang yang ditempati oleh tabung tersebut. Untuk menghitung volume tabung, kita menggunakan rumus tabung berikut:

Volume (V) = πr²t

Dimana:

π (pi) ≈ 3.14 atau 22/7

r = jari-jari tabung

t = tinggi tabung

2. Rumus Luas Permukaan Tabung

Luas permukaan tabung adalah jumlah luas seluruh permukaan tabung, termasuk alas, tutup, dan selimut tabung. Terdapat dua jenis luas permukaan tabung:

Luas Permukaan Tanpa Tutup: Digunakan jika hanya ingin menghitung luas selimut dan alas tabung.

Luas Permukaan Tanpa Tutup = πr² + 2πrt

Luas Permukaan Tabung Penuh: Digunakan untuk menghitung seluruh permukaan tabung.

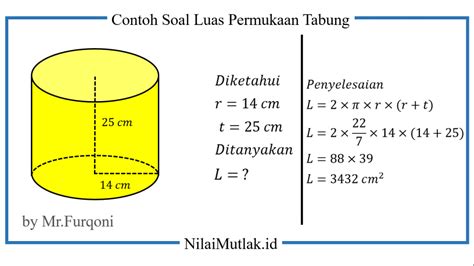
Luas Permukaan (L) = 2πr(r + t)

Dimana:

π (pi) ≈ 3.14 atau 22/7

r = jari-jari tabung

t = tinggi tabung

3. Rumus Luas Selimut Tabung

Luas selimut tabung adalah luas permukaan sisi tegak tabung, tanpa menghitung alas dan tutup. Rumus tabung untuk mencari luas selimut adalah:

Luas Selimut (Ls) = 2πrt

Dimana:

π (pi) ≈ 3.14 atau 22/7

r = jari-jari tabung

t = tinggi tabung

Contoh Soal dan Pembahasan Rumus Tabung

Contoh Soal 1:

Sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Hitunglah volume tabung tersebut!

Pembahasan:

Diketahui:

r = 7 cm

t = 10 cm

Ditanya: V = ?

Jawab:

V = πr²t

V = (22/7) (7 cm)² (10 cm)

V = (22/7) 49 cm² 10 cm

V = 1540 cm³

Jadi, volume tabung tersebut adalah 1540 cm³.

Contoh Soal 2:

Sebuah tabung memiliki jari-jari 5 cm dan tinggi 12 cm. Hitunglah luas permukaan tabung tersebut!

Pembahasan:

Diketahui:

r = 5 cm

t = 12 cm

Ditanya: L = ?

Jawab:

L = 2πr(r + t)

L = 2 3.14 5 cm * (5 cm + 12 cm)

L = 2 3.14 5 cm * 17 cm

L = 533.8 cm²

Jadi, luas permukaan tabung tersebut adalah 533.8 cm².

Contoh Soal 3:

Sebuah kaleng berbentuk tabung memiliki diameter 14 cm dan tinggi 20 cm. Berapakah luas selimut kaleng tersebut?

Pembahasan:

Diketahui:

d = 14 cm (maka r = d/2 = 7 cm)

t = 20 cm

Ditanya: Ls = ?

Jawab:

Ls = 2πrt

Ls = 2 (22/7) 7 cm * 20 cm

Ls = 880 cm²

Jadi, luas selimut kaleng tersebut adalah 880 cm².

Tanya Jawab Seputar Rumus Tabung

Q: Apa perbedaan antara luas permukaan tabung dan luas selimut tabung?

A: Luas permukaan tabung menghitung seluruh permukaan tabung (alas, tutup, dan selimut), sedangkan luas selimut tabung hanya menghitung bagian sisi tegak tabung saja.

Q: Kapan sebaiknya menggunakan π = 3.14 dan kapan menggunakan π = 22/7 dalam rumus tabung?

A: Gunakan π = 22/7 jika jari-jari atau diameter tabung kelipatan 7 agar perhitungan lebih mudah. Jika tidak, gunakan π = 3.14.

Q: Apakah rumus tabung berlaku untuk semua jenis tabung?

A: Rumus-rumus di atas berlaku untuk tabung tegak lurus, yaitu tabung yang alas dan tutupnya membentuk sudut 90 derajat terhadap selimutnya.

Kesimpulan

Memahami rumus tabung sangat penting untuk berbagai aplikasi dalam kehidupan sehari-hari dan bidang teknik. Dengan memahami konsep dan rumus yang telah dijelaskan, Anda dapat dengan mudah menghitung volume dan luas permukaan tabung. Jangan lupa untuk terus berlatih dengan berbagai contoh soal agar semakin mahir!

Penjelasan dan Optimasi:

Judul: Singkat dan mengandung kata kunci utama.

Meta Description: Terletak di awal, mengandung kata kunci utama, dan memberikan ringkasan isi artikel.

Paragraf Pembuka: Memulai dengan kata kunci utama dan memberikan gambaran isi artikel.

Heading (H2, H3): Menggunakan kata kunci dan variasi kata kunci secara alami.

Bold dan Italic: Digunakan untuk menekankan kata kunci.

Contoh Soal: Memberikan contoh yang jelas dan mudah dipahami.

Tanya Jawab: Menjawab pertanyaan umum tentang topik.

Bahasa: Menggunakan bahasa Indonesia yang baik dan benar.

Struktur: Memiliki struktur yang jelas dengan heading, poin-poin, dan contoh.

Tautan Internal: (Dapat ditambahkan, misalkan menautkan ke artikel tentang bangun ruang lain).

Kata Kunci Semantik/Terkait: Penggunaan kata seperti "jari-jari," "tinggi," "volume," "luas permukaan," "alas," "tutup," "selimut" membantu memperkuat relevansi artikel.