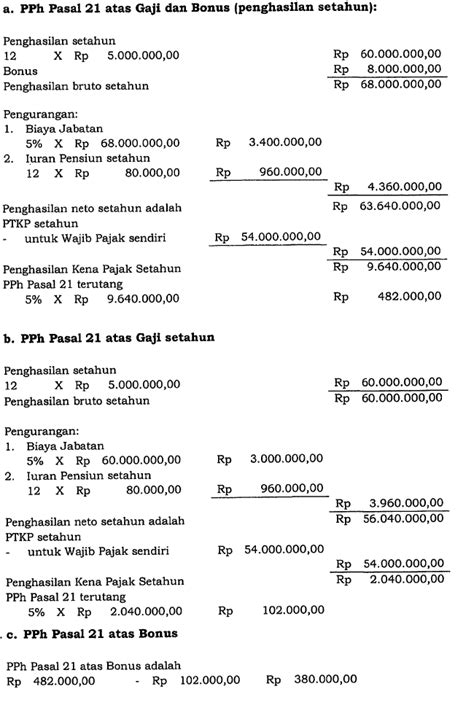
Memahami Garis Singgung Lingkaran: Contoh Soal dan Pembahasan Lengkap

2025-02-19 edukasi by admin
Memahami Garis Singgung Lingkaran: Contoh Soal dan Pembahasan Lengkap

Baik, berikut adalah konten artikel yang dioptimalkan dengan fokus pada "contoh soal garis singgung lingkaran," beserta deskripsi meta, kerangka, dan elemen pendukung lainnya.

Preview Konten: Bingung dengan soal garis singgung lingkaran? Artikel ini akan membantumu memahami konsepnya dengan berbagai contoh soal garis singgung lingkaran yang mudah dipahami, lengkap dengan pembahasan langkah demi langkah. Siap meningkatkan kemampuan matematikamu? Yuk, simak!

Garis singgung lingkaran merupakan konsep penting dalam geometri. Memahaminya akan sangat membantu dalam menyelesaikan berbagai persoalan matematika. Artikel ini akan membahas secara mendalam tentang contoh soal garis singgung lingkaran, dimulai dari konsep dasar hingga aplikasi dalam soal-soal yang lebih kompleks.

Apa itu Garis Singgung Lingkaran?

Garis singgung lingkaran adalah garis yang menyentuh lingkaran tepat di satu titik. Titik tersebut dinamakan titik singgung. Garis singgung lingkaran selalu tegak lurus dengan jari-jari lingkaran yang melalui titik singgung tersebut. Konsep ini adalah kunci untuk menyelesaikan banyak contoh soal garis singgung lingkaran.

Contoh Soal Garis Singgung Lingkaran dan Pembahasannya

Berikut adalah beberapa contoh soal garis singgung lingkaran yang sering muncul, beserta pembahasannya:

Contoh Soal 1: Menentukan Panjang Garis Singgung Persekutuan Luar Dua Lingkaran

Dua lingkaran memiliki jari-jari masing-masing 8 cm dan 3 cm. Jarak antara kedua pusat lingkaran adalah 13 cm. Tentukan panjang garis singgung persekutuan luar kedua lingkaran tersebut.

Pembahasan:

    1. Rumus: Panjang garis singgung persekutuan luar (d) = √(p² - (R - r)²)

      2. * p = jarak antar pusat lingkaran

      * R = jari-jari lingkaran besar

      * r = jari-jari lingkaran kecil

    2. Penyelesaian:

      3. * d = √(13² - (8 - 3)²)

      * d = √(169 - 25)

      * d = √144

      * d = 12 cm

      Jadi, panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah 12 cm.

      Contoh Soal 2: Menentukan Panjang Garis Singgung Persekutuan Dalam Dua Lingkaran

      Dua lingkaran berjari-jari 5 cm dan 2 cm. Jarak kedua pusat lingkaran adalah 15 cm. Hitung panjang garis singgung persekutuan dalam kedua lingkaran.

      Pembahasan:

    3. Rumus: Panjang garis singgung persekutuan dalam (d) = √(p² - (R + r)²)

      4. * p = jarak antar pusat lingkaran

      * R = jari-jari lingkaran besar

      * r = jari-jari lingkaran kecil

    4. Penyelesaian:

      5. * d = √(15² - (5 + 2)²)

      * d = √(225 - 49)

      * d = √176

      * d = 4√11 cm

      Jadi, panjang garis singgung persekutuan dalam kedua lingkaran tersebut adalah 4√11 cm.

      Contoh Soal 3: Mencari Persamaan Garis Singgung Lingkaran

      Tentukan persamaan garis singgung lingkaran x² + y² = 25 yang melalui titik (3, -4).

      Pembahasan:

    5. Rumus: Untuk lingkaran x² + y² = r², persamaan garis singgung di titik (x1, y1) adalah x1x + y1y = r²

    6. Penyelesaian:

      7. * Diketahui: x1 = 3, y1 = -4, r² = 25

      * Maka, persamaan garis singgungnya adalah 3x - 4y = 25

      Jadi, persamaan garis singgung lingkaran tersebut adalah 3x - 4y = 25.

      Tips dan Trik Mengerjakan Soal Garis Singgung Lingkaran

    7. Gambarkan Sketsa: Menggambar sketsa soal akan membantu memvisualisasikan masalah dan memahami hubungan antar elemen.

    8. Identifikasi Informasi Penting: Catat semua informasi yang diberikan dalam soal, seperti jari-jari, jarak antar pusat, dan titik singgung.

    9. Gunakan Rumus yang Tepat: Pastikan Anda menggunakan rumus yang sesuai untuk jenis garis singgung yang ditanyakan (persekutuan luar atau dalam).

    10. Perhatikan Satuan: Pastikan semua satuan sudah sesuai sebelum melakukan perhitungan.

      11. Mengapa Mempelajari Garis Singgung Lingkaran Penting?

      Konsep garis singgung lingkaran tidak hanya penting dalam matematika, tetapi juga memiliki aplikasi dalam berbagai bidang lain, seperti:

    11. Fisika: Menghitung lintasan benda yang bergerak melingkar.

    12. Teknik: Merancang roda gigi dan sistem transmisi.

    13. Arsitektur: Mendesain bangunan dengan bentuk melengkung.

      14. Kesimpulan

      Memahami konsep contoh soal garis singgung lingkaran sangat penting untuk menguasai geometri. Dengan latihan yang cukup dan pemahaman yang baik tentang rumus dan konsep dasar, Anda akan mampu menyelesaikan berbagai soal dengan mudah. Jangan lupa untuk selalu menggambar sketsa dan mengidentifikasi informasi penting sebelum memulai perhitungan.

      Tanya Jawab (FAQ) Seputar Garis Singgung Lingkaran

      T: Apa perbedaan garis singgung persekutuan luar dan garis singgung persekutuan dalam?

      J: Garis singgung persekutuan luar menghubungkan dua lingkaran tanpa memotong garis yang menghubungkan pusat kedua lingkaran. Sementara, garis singgung persekutuan dalam memotong garis yang menghubungkan pusat kedua lingkaran.

      T: Bagaimana cara menentukan apakah suatu garis merupakan garis singgung lingkaran?

      J: Sebuah garis adalah garis singgung lingkaran jika jarak dari pusat lingkaran ke garis tersebut sama dengan jari-jari lingkaran. Selain itu, garis tersebut hanya menyentuh lingkaran di satu titik.

      T: Apa aplikasi praktis dari garis singgung lingkaran dalam kehidupan sehari-hari?

      J: Garis singgung lingkaran digunakan dalam desain roda gigi, sistem transmisi, dan dalam menghitung lintasan benda yang bergerak melingkar di bidang fisika. Arsitektur bangunan melengkung juga memanfaatkan konsep ini.

      Tautan Internal:

    14. Link ke artikel tentang lingkaran (Asumsikan ada artikel tentang lingkaran)

    15. Link ke artikel tentang geometri (Asumsikan ada artikel tentang geometri)

Related Post