Contoh Soal SPLDV (Sistem Persamaan Linear Dua Variabel) Beserta Pembahasannya
Oke, berikut adalah draf konten artikel mengenai contoh soal SPLDV, dioptimalkan untuk SEO dan pembaca, dengan mengikuti semua instruksi yang diberikan:
Sistem Persamaan Linear Dua Variabel (SPLDV) adalah materi penting dalam matematika. Bingung dengan contoh soal SPLDV? Artikel ini akan membantu Anda memahami konsep SPLDV dan cara menyelesaikan berbagai jenis soal dengan mudah. Kami akan menyajikan berbagai contoh soal SPLDV yang disertai pembahasan lengkap, sehingga Anda dapat meningkatkan kemampuan dalam menyelesaikan permasalahan yang berkaitan dengan SPLDV. Mari kita mulai!
Apa Itu Sistem Persamaan Linear Dua Variabel (SPLDV)?
SPLDV adalah dua persamaan linear yang memiliki dua variabel (biasanya x dan y). Solusi SPLDV adalah pasangan nilai x dan y yang memenuhi kedua persamaan tersebut secara bersamaan.
Metode Penyelesaian SPLDV
Ada beberapa metode untuk menyelesaikan SPLDV, di antaranya:
- Metode Grafik: Menggambar kedua garis dan mencari titik potongnya.
- Metode Substitusi: Menyelesaikan satu persamaan untuk satu variabel, kemudian mensubstitusikan hasilnya ke persamaan lain.
- Metode Eliminasi: Menghilangkan salah satu variabel dengan menjumlahkan atau mengurangkan kedua persamaan.
- Metode Eliminasi:
- Membuat Model Matematika:
- Metode Substitusi:
- x + y = 4
- 2x - y = 2
- Membuat Grafik:
- Pahami Konsep Dasar: Pastikan Anda memahami definisi SPLDV dan metode penyelesaiannya.
- Pilih Metode yang Tepat: Pertimbangkan metode mana yang paling efisien untuk soal tertentu.
- Teliti dalam Perhitungan: Hindari kesalahan perhitungan agar mendapatkan hasil yang akurat.
- Latihan Soal: Semakin banyak latihan, semakin terampil Anda dalam menyelesaikan soal SPLDV.
- Satu solusi (jika kedua garis berpotongan).
- Tidak ada solusi (jika kedua garis sejajar).
- Tak hingga banyak solusi (jika kedua garis berimpit).
Contoh Soal SPLDV dan Pembahasannya
Berikut adalah beberapa contoh soal SPLDV beserta pembahasannya menggunakan berbagai metode penyelesaian:
Contoh Soal 1:
Tentukan himpunan penyelesaian dari sistem persamaan berikut:
x + y = 5
x - y = 1
Pembahasan:
Jumlahkan kedua persamaan:
(x + y) + (x - y) = 5 + 1
2x = 6
x = 3
Substitusikan nilai x = 3 ke salah satu persamaan, misalnya x + y = 5:
3 + y = 5
y = 2
Jadi, himpunan penyelesaiannya adalah {(3, 2)}.
Contoh Soal 2:
Harga 2 buah buku dan 3 buah pensil adalah Rp13.000,00. Harga 3 buah buku dan 1 buah pensil adalah Rp11.000,00. Tentukan harga sebuah buku dan sebuah pensil.
Pembahasan:
Misalkan harga sebuah buku adalah x dan harga sebuah pensil adalah y. Maka, kita dapat membuat model matematika sebagai berikut:
2x + 3y = 13.000
3x + y = 11.000
Selesaikan persamaan kedua untuk y:
y = 11.000 - 3x
Substitusikan nilai y ke persamaan pertama:
2x + 3(11.000 - 3x) = 13.000
2x + 33.000 - 9x = 13.000
-7x = -20.000
x = 2.857,14 (dibulatkan menjadi 2.857)
Substitusikan nilai x = 2.857 ke persamaan y = 11.000 - 3x:
y = 11.000 - 3(2.857)
y = 2.429
Jadi, harga sebuah buku adalah Rp2.857,00 dan harga sebuah pensil adalah Rp2.429,00 (nilai ini adalah hasil pembulatan, solusi yang tepat membutuhkan perhitungan yang lebih presisi).
Contoh Soal 3:
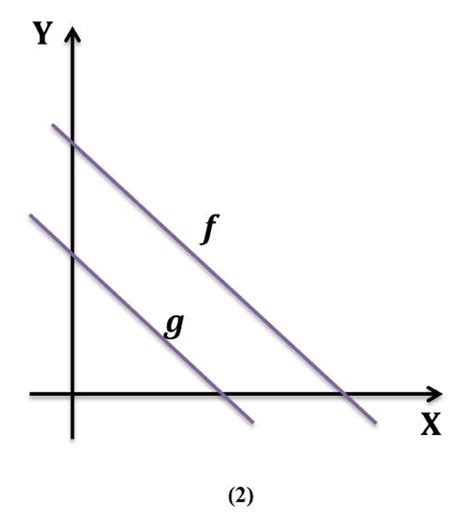
Dengan menggunakan metode grafik, tentukan himpunan penyelesaian dari:
Pembahasan:
Ubahlah kedua persamaan ke bentuk y = mx + c:
* x + y = 4 => y = -x + 4
* 2x - y = 2 => y = 2x - 2
Gambarkan kedua garis pada bidang koordinat. Titik potong kedua garis adalah solusi dari SPLDV tersebut. Dari grafik (yang tidak bisa ditampilkan di sini), titik potongnya adalah (2, 2).
Jadi, himpunan penyelesaiannya adalah {(2, 2)}.
Tips dan Trik Menyelesaikan Soal SPLDV
Tanya Jawab Seputar SPLDV
Q: Kapan sebaiknya saya menggunakan metode eliminasi?
A: Metode eliminasi sangat efektif jika koefisien salah satu variabel pada kedua persamaan sama atau merupakan kelipatan, sehingga mudah untuk dihilangkan dengan menjumlahkan atau mengurangkan kedua persamaan.
Q: Apa yang terjadi jika dua garis pada metode grafik sejajar?
A: Jika dua garis sejajar, maka SPLDV tidak memiliki solusi. Ini berarti tidak ada pasangan nilai x dan y yang memenuhi kedua persamaan secara bersamaan.
Q: Apakah SPLDV selalu memiliki satu solusi?
A: Tidak. SPLDV bisa memiliki:
Kesimpulan
Memahami contoh soal SPLDV adalah kunci untuk menguasai materi ini. Dengan latihan yang cukup dan pemahaman yang mendalam mengenai metode penyelesaian, Anda akan mampu menyelesaikan berbagai permasalahan SPLDV dengan mudah. Selamat belajar!
(Tautan Internal: Jika ada artikel lain tentang sistem persamaan, tautkan di sini.)