Contoh Soal Persamaan Garis Lurus: Panduan Lengkap dengan Pembahasan

2025-02-17 Edukasi by admin

Oke, berikut adalah konten artikel tentang contoh soal persamaan garis lurus, dioptimalkan untuk SEO, dan ditulis dalam bahasa Indonesia yang baik dan benar:

`markdown

Preview: Persamaan garis lurus seringkali menjadi momok bagi sebagian siswa. Padahal, dengan memahami konsep dasarnya dan berlatih mengerjakan contoh soal persamaan garis lurus, kamu akan mampu menaklukkannya dengan mudah! Artikel ini akan menyajikan berbagai contoh soal persamaan garis lurus yang lengkap dengan pembahasan detail, siap membantu kamu meningkatkan pemahaman.

Memahami Persamaan Garis Lurus: Konsep Dasar

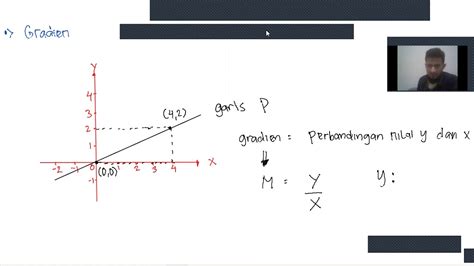
Sebelum membahas contoh soal persamaan garis lurus, mari kita review sedikit tentang konsep dasarnya. Persamaan garis lurus adalah persamaan matematika yang jika digambarkan pada koordinat kartesius akan membentuk sebuah garis lurus. Bentuk umumnya adalah:

y = mx + c

Dimana:

y: Variabel dependen (nilai y tergantung pada nilai x)

x: Variabel independen

m: Gradien (kemiringan garis)

c: Intersep y (titik potong garis dengan sumbu y)

Memahami konsep gradien sangat penting dalam menyelesaikan contoh soal persamaan garis lurus. Gradien (m) menunjukkan seberapa curam garis tersebut. Semakin besar nilai gradien, semakin curam garisnya.

Contoh Soal Persamaan Garis Lurus dan Pembahasannya

Berikut adalah beberapa contoh soal persamaan garis lurus yang sering muncul, beserta pembahasan detailnya:

Contoh Soal 1: Menentukan Gradien

Soal: Tentukan gradien garis yang melalui titik (2, 3) dan (4, 7).

Pembahasan:

Rumus gradien (m) adalah:

m = (y2 - y1) / (x2 - x1)

Dimana:

(x1, y1) = (2, 3)

(x2, y2) = (4, 7)

Maka:

m = (7 - 3) / (4 - 2) = 4 / 2 = 2

Jawaban: Gradien garis tersebut adalah 2.

Contoh Soal 2: Menentukan Persamaan Garis Lurus

Soal: Tentukan persamaan garis lurus yang memiliki gradien 3 dan melalui titik (1, 2).

Pembahasan:

Kita bisa menggunakan rumus titik-gradien:

y - y1 = m(x - x1)

Dimana:

m = 3

(x1, y1) = (1, 2)

Maka:

y - 2 = 3(x - 1)

y - 2 = 3x - 3

y = 3x - 1

Jawaban: Persamaan garis lurus tersebut adalah y = 3x - 1.

Contoh Soal 3: Menentukan Persamaan Garis Lurus yang Melalui Dua Titik

Soal: Tentukan persamaan garis lurus yang melalui titik (0, -4) dan (5, 0).

Pembahasan:

Pertama, kita cari gradiennya:

m = (0 - (-4)) / (5 - 0) = 4 / 5

Kemudian, kita bisa menggunakan rumus titik-gradien dengan salah satu titik (misalnya (5,0)):

y - 0 = (4/5)(x - 5)

y = (4/5)x - 4

Jawaban: Persamaan garis lurus tersebut adalah y = (4/5)x - 4.

Contoh Soal 4: Menentukan Intersep Garis Lurus

Soal: Suatu garis lurus memiliki persamaan 2y = 4x + 8. Tentukan intersep y (titik potong garis dengan sumbu y) dan gradiennya.

Pembahasan:

Ubah persamaan ke bentuk y = mx + c:

y = 2x + 4

Dari persamaan ini, kita bisa langsung melihat bahwa:

Gradien (m) = 2

Intersep y (c) = 4

Jawaban: Gradien garis adalah 2 dan intersep y adalah 4.

Contoh Soal 5: Persamaan Garis Sejajar

Soal: Tentukan persamaan garis yang sejajar dengan garis y = 2x + 3 dan melalui titik (1, -1).

Pembahasan:

Garis yang sejajar memiliki gradien yang sama. Jadi, gradien garis yang kita cari adalah 2. Gunakan rumus titik gradien.

y - (-1) = 2 (x-1)

y + 1 = 2x - 2

y = 2x - 3

Jawaban: Persamaan garis yang sejajar adalah y = 2x - 3.

Tips Mengerjakan Soal Persamaan Garis Lurus

Pahami Konsep Dasar: Kuasai rumus gradien, persamaan garis lurus (y = mx + c), dan rumus titik-gradien.

Visualisasikan: Gambarlah garis lurus pada koordinat kartesius untuk membantu memahami soal.

Berlatih Terus: Semakin banyak contoh soal persamaan garis lurus yang kamu kerjakan, semakin terlatih kamu dalam menyelesaikannya.

Perhatikan Detail: Pastikan kamu membaca soal dengan teliti dan memahami apa yang ditanyakan.

Tanya Jawab (FAQ) Seputar Persamaan Garis Lurus

Q: Apa itu gradien dan bagaimana cara menghitungnya?

A: Gradien adalah kemiringan suatu garis lurus. Cara menghitungnya adalah dengan rumus: m = (y2 - y1) / (x2 - x1), dimana (x1, y1) dan (x2, y2) adalah dua titik yang dilalui garis tersebut.

Q: Bagaimana cara menentukan persamaan garis lurus jika diketahui gradien dan satu titik?

A: Gunakan rumus titik-gradien: y - y1 = m(x - x1), dimana m adalah gradien dan (x1, y1) adalah titik yang diketahui.

Q: Apa perbedaan antara persamaan garis lurus sejajar dan tegak lurus?

A: Garis sejajar memiliki gradien yang sama. Garis tegak lurus memiliki gradien yang merupakan negatif kebalikan dari gradien garis lainnya. Misalnya, jika gradien garis pertama adalah m, maka gradien garis tegak lurusnya adalah -1/m.

Kesimpulan

Dengan memahami konsep dasar dan berlatih mengerjakan berbagai contoh soal persamaan garis lurus, kamu pasti bisa menguasai materi ini. Jangan takut untuk mencoba dan jangan menyerah jika menemui kesulitan. Selamat belajar!

Catatan: