Contoh Soal Luas Tembereng: Panduan Lengkap

2025-02-13 uncategorized by admin
Contoh Soal Luas Tembereng: Panduan Lengkap

H2: Memahami Konsep Luas Tembereng

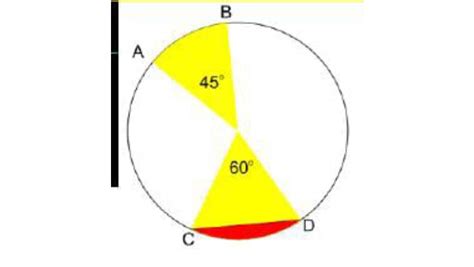
Sebelum kita masuk ke contoh soal luas tembereng, mari kita pahami dulu apa itu tembereng. Tembereng adalah daerah pada lingkaran yang dibatasi oleh tali busur dan busur lingkaran. Menghitung luas tembereng membutuhkan pemahaman tentang geometri lingkaran, khususnya mengenai luas juring dan luas segitiga. Artikel ini akan memberikan contoh soal luas tembereng yang beragam, disertai penjelasan langkah demi langkah. Siap untuk menguasai perhitungan luas tembereng?

H2: Rumus Menghitung Luas Tembereng

Rumus umum untuk menghitung luas tembereng adalah:

Luas Tembereng = Luas Juring - Luas Segitiga

di mana:

    1. Luas Juring = (θ/360°) × πr² (θ adalah sudut pusat dalam derajat, r adalah jari-jari lingkaran)

    2. Luas Segitiga = (1/2) × r² × sin θ

      3. H2: Contoh Soal Luas Tembereng dan Penyelesaiannya

      Berikut beberapa contoh soal luas tembereng beserta penyelesaiannya:

      Contoh 1:

      Sebuah lingkaran memiliki jari-jari 10 cm. Hitunglah luas tembereng yang dibentuk oleh tali busur dengan sudut pusat 60°.

      Penyelesaian:

    3. Hitung luas juring: Luas Juring = (60°/360°) × π(10)² = (1/6) × 100π = 50π/3 cm²

    4. Hitung luas segitiga: Luas Segitiga = (1/2) × 10² × sin 60° = 50 × (√3/2) = 25√3 cm²

    5. Hitung luas tembereng: Luas Tembereng = Luas Juring - Luas Segitiga = (50π/3) - 25√3 cm² ≈ 12.27 cm²

      6. Contoh 2:

      Suatu lingkaran memiliki jari-jari 7 cm dan sudut pusat 120°. Tentukan luas tembereng yang terbentuk.

      Penyelesaian:

    6. Hitung luas juring: Luas Juring = (120°/360°) × π(7)² = (1/3) × 49π = 49π/3 cm²

    7. Hitung luas segitiga: Luas Segitiga = (1/2) × 7² × sin 120° = 49/2 × (√3/2) = 49√3/4 cm²

    8. Hitung luas tembereng: Luas Tembereng = Luas Juring - Luas Segitiga = (49π/3) - (49√3/4) cm² ≈ 20.82 cm²

      9. H2: Tips dan Trik Menghitung Luas Tembereng

    9. Pastikan Anda memahami rumus luas juring dan luas segitiga.

    10. Perhatikan satuan yang digunakan dalam perhitungan.

    11. Gunakan kalkulator untuk mempermudah perhitungan, terutama untuk nilai π dan akar pangkat.

    12. Latih terus dengan berbagai contoh soal luas tembereng untuk meningkatkan pemahaman dan kecepatan perhitungan.

H2: Pertanyaan dan Jawaban (FAQ)

Q: Apa perbedaan antara juring dan tembereng?

A: Juring adalah daerah pada lingkaran yang dibatasi oleh dua jari-jari dan busur lingkaran. Sedangkan tembereng adalah daerah pada lingkaran yang dibatasi oleh tali busur dan busur lingkaran.

Q: Apa yang dimaksud dengan tali busur?

A: Tali busur adalah ruas garis yang menghubungkan dua titik pada keliling lingkaran.

Q: Bagaimana jika sudut pusat lebih dari 180°?

A: Rumus tetap sama, namun perhatikan bahwa luas segitiga akan lebih besar dari luas juring pada setengah lingkaran. Luas tembereng akan menjadi negatif, sehingga Anda perlu mengambil nilai absolutnya.

Dengan pemahaman yang baik tentang rumus dan latihan yang cukup, Anda akan dapat dengan mudah menyelesaikan soal-soal luas tembereng. Selamat mencoba!

Related Post