Contoh Soal Kesebangunan dan Kekongruenan: Panduan Lengkap dan Pembahasan

2025-02-19 edukasi by admin
Contoh Soal Kesebangunan dan Kekongruenan: Panduan Lengkap dan Pembahasan

Oke, berikut adalah konten artikel yang dioptimalkan untuk SEO dengan fokus pada contoh soal kesebangunan dan kekongruenan, disusun sesuai dengan instruksi yang diberikan:

(Preview Konten): Bingung dengan soal-soal kesebangunan dan kekongruenan? Artikel ini hadir untuk membantumu! Dilengkapi dengan contoh soal yang beragam dan pembahasan mendalam, kamu akan lebih mudah memahami konsepnya dan siap menghadapi ujian. Mari kita pelajari bersama!

Memahami Konsep Dasar Kesebangunan dan Kekongruenan

Sebelum membahas contoh soal kesebangunan dan kekongruenan, mari kita pahami terlebih dahulu konsep dasarnya. Kesebangunan dan kekongruenan adalah dua konsep penting dalam geometri yang seringkali membingungkan.

    1. Kesebangunan (Similarity): Dua bangun datar dikatakan sebangun jika bentuknya sama, tetapi ukurannya boleh berbeda. Syaratnya adalah sudut-sudut yang bersesuaian sama besar, dan sisi-sisi yang bersesuaian memiliki perbandingan yang sama. Konsep ini penting dalam memahami skala peta, miniatur, dan model.

    2. Kekongruenan (Congruence): Dua bangun datar dikatakan kongruen jika bentuk dan ukurannya sama persis. Syaratnya adalah sudut-sudut yang bersesuaian sama besar, dan sisi-sisi yang bersesuaian sama panjang. Konsep ini banyak diterapkan dalam konstruksi dan desain.

      3. Contoh Soal Kesebangunan dan Pembahasan

      Berikut adalah beberapa contoh soal kesebangunan yang disertai dengan pembahasannya:

      Contoh Soal 1:

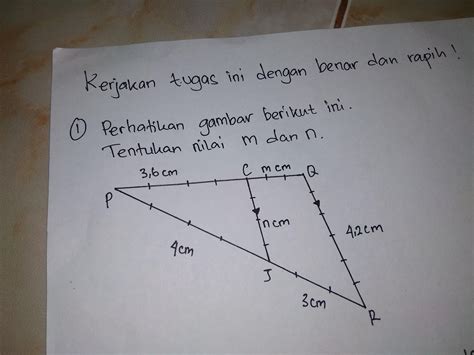
      Dua buah persegi panjang, ABCD dan PQRS, sebangun. Jika panjang AB = 12 cm, lebar BC = 8 cm, dan panjang PQ = 18 cm, tentukan lebar QR.

      Pembahasan:

      Karena ABCD dan PQRS sebangun, maka:

      AB/PQ = BC/QR

      12/18 = 8/QR

      QR = (8 * 18) / 12

      QR = 12 cm

      Contoh Soal 2:

      Perhatikan gambar berikut: (Sertakan gambar dua segitiga sebangun, ABC dan ADE, dengan DE sejajar BC)

      Jika AD = 4 cm, DB = 6 cm, dan AE = 5 cm, tentukan panjang EC.

      Pembahasan:

      Karena DE sejajar BC, maka segitiga ADE sebangun dengan segitiga ABC. Sehingga:

      AD/AB = AE/AC

      4/(4+6) = 5/(5+EC)

      4/10 = 5/(5+EC)

      2/5 = 5/(5+EC)

      2(5+EC) = 25

      10 + 2EC = 25

      2EC = 15

      EC = 7.5 cm

      Contoh Soal 3:

      Sebuah foto berukuran 4 cm x 6 cm akan diperbesar sehingga lebarnya menjadi 12 cm. Berapakah panjang foto setelah diperbesar?

      Pembahasan:

      Karena foto diperbesar secara sebangun, maka:

      Lebar awal / Lebar akhir = Panjang awal / Panjang akhir

      4 / 12 = 6 / Panjang akhir

      Panjang akhir = (6 * 12) / 4

      Panjang akhir = 18 cm

      Contoh Soal Kekongruenan dan Pembahasan

      Berikut adalah beberapa contoh soal kekongruenan yang disertai dengan pembahasannya:

      Contoh Soal 1:

      Diberikan dua segitiga ABC dan PQR. Jika AB = PQ, BC = QR, dan AC = PR, buktikan bahwa segitiga ABC kongruen dengan segitiga PQR.

      Pembahasan:

      Karena ketiga sisi segitiga ABC sama panjang dengan ketiga sisi segitiga PQR (AB = PQ, BC = QR, AC = PR), maka berdasarkan kriteria Sisi-Sisi-Sisi (SSS), segitiga ABC kongruen dengan segitiga PQR.

      Contoh Soal 2:

      Perhatikan gambar berikut: (Sertakan gambar dua segitiga siku-siku, ABC dan DEF, dengan AB = DE dan ∠B = ∠E = 90°)

      Jika AB = 8 cm, BC = 6 cm, DE = 8 cm, dan EF = 6 cm, buktikan bahwa segitiga ABC kongruen dengan segitiga DEF.

      Pembahasan:

      Karena AB = DE dan BC = EF, serta kedua segitiga merupakan segitiga siku-siku, maka berdasarkan kriteria Sisi-Sudut-Sisi (SAS), segitiga ABC kongruen dengan segitiga DEF.

      Contoh Soal 3:

      Diketahui segitiga KLM sama kaki dengan KL = KM. Titik N adalah titik tengah LM. Buktikan bahwa segitiga KLN kongruen dengan segitiga KMN.

      Pembahasan:

    3. KL = KM (diketahui)

    4. LN = MN (karena N titik tengah LM)

    5. KN = KN (sisi sekutu)

      6. Berdasarkan kriteria Sisi-Sisi-Sisi (SSS), segitiga KLN kongruen dengan segitiga KMN.

      Tips Mengerjakan Soal Kesebangunan dan Kekongruenan

    6. Pahami Definisi: Pastikan kamu benar-benar memahami perbedaan antara kesebangunan dan kekongruenan.

    7. Identifikasi Sisi dan Sudut yang Bersesuaian: Ini sangat penting untuk menentukan perbandingan yang tepat (pada kesebangunan) atau untuk membuktikan kesamaan (pada kekongruenan).

    8. Gunakan Kriteria Kesebangunan dan Kekongruenan: Kuasai kriteria Sisi-Sisi-Sisi (SSS), Sisi-Sudut-Sisi (SAS), Sudut-Sisi-Sudut (ASA), dan Sudut-Sudut-Sudut (AAA) untuk membuktikan kekongruenan atau kesebangunan.

    9. Latihan Soal: Semakin banyak kamu berlatih, semakin terbiasa kamu dengan berbagai tipe soal.

Kesimpulan

Memahami contoh soal kesebangunan dan kekongruenan adalah kunci untuk menguasai materi geometri. Dengan pemahaman yang baik tentang konsep dasar dan kriteria kesebangunan dan kekongruenan, serta dengan banyak berlatih, kamu pasti bisa menyelesaikan soal-soal dengan mudah. Selamat belajar!

Tanya Jawab (FAQ)

Q: Apa perbedaan utama antara kesebangunan dan kekongruenan?

A: Kesebangunan berarti bentuk sama, ukuran boleh berbeda, sedangkan kekongruenan berarti bentuk dan ukuran harus sama persis.

Q: Kriteria apa saja yang bisa digunakan untuk membuktikan kekongruenan dua segitiga?

A: Kriteria yang umum digunakan adalah Sisi-Sisi-Sisi (SSS), Sisi-Sudut-Sisi (SAS), dan Sudut-Sisi-Sudut (ASA).

Q: Bagaimana cara menentukan sisi-sisi yang bersesuaian pada bangun yang sebangun?

A: Perhatikan sudut-sudut yang sama besar. Sisi yang berada di antara dua sudut yang sama besar adalah sisi yang bersesuaian.

Related Post