Contoh Soal Integral Tak Tentu: Panduan Lengkap

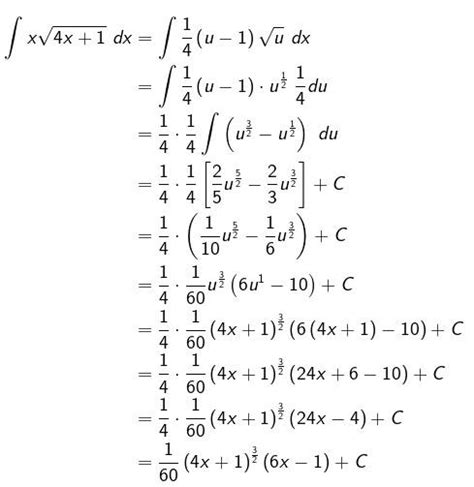
Contoh Soal Integral Tak Tentu dan Pembahasannya

Artikel ini akan membahas berbagai contoh soal integral tak tentu, lengkap dengan pembahasan langkah demi langkah. Mempelajari integral tak tentu sangat penting dalam kalkulus dan aplikasi-aplikasinya. Baik Anda siswa SMA, mahasiswa, atau siapapun yang ingin mempelajari integral, artikel ini akan sangat membantu. Kita akan mempelajari berbagai teknik dan trik untuk menyelesaikan soal-soal integral tak tentu.

Apa itu Integral Tak Tentu?

Sebelum kita masuk ke contoh soal integral tak tentu, mari kita ulas kembali definisi integral tak tentu. Integral tak tentu dari suatu fungsi f(x) adalah suatu fungsi F(x) yang turunannya sama dengan f(x). Dengan kata lain, ∫f(x)dx = F(x) + C, dimana C adalah konstanta integrasi. Konstanta integrasi ini penting karena turunan dari konstanta selalu nol.

Contoh Soal Integral Tak Tentu Dasar

Berikut beberapa contoh soal integral tak tentu dasar dan pembahasannya:

1. ∫ x² dx

1. Penyelesaian: Menggunakan aturan integral pangkat, kita dapatkan:

∫ x² dx = (x³/3) + C

2. ∫ (3x + 2) dx

2. Penyelesaian: Kita dapat mengintegralkan suku per suku:

∫ (3x + 2) dx = (3x²/2) + 2x + C

3. ∫ 1/x dx

3. Penyelesaian: Integral dari 1/x adalah ln|x| (natural logarithm dari nilai absolut x):

∫ 1/x dx = ln|x| + C

Contoh Soal Integral Tak Tentu yang Lebih Kompleks

Berikut contoh soal integral tak tentu yang sedikit lebih menantang:

1. ∫ (x³ + 2x - 5) dx

4. Penyelesaian: Kita mengintegralkan setiap suku:

∫ (x³ + 2x - 5) dx = (x⁴/4) + x² - 5x + C

2. ∫ (sin x + cos x) dx

5. Penyelesaian: Ingatlah rumus turunan dan integral trigonometri:

∫ (sin x + cos x) dx = -cos x + sin x + C

3. ∫ e^x dx

6. Penyelesaian: Integral dari e^x adalah e^x itu sendiri:

∫ e^x dx = e^x + C

Teknik Integrasi Lainnya

Ada berbagai teknik integrasi lain yang lebih kompleks seperti substitusi, integrasi parsial, dan integrasi trigonometri. Artikel-artikel selanjutnya akan membahas teknik-teknik ini secara lebih detail. Link ke artikel tentang substitusi.

Tanya Jawab

Q: Apa perbedaan antara integral tentu dan integral tak tentu?

A: Integral tentu menghasilkan nilai numerik yang merepresentasikan luas area di bawah kurva, sedangkan integral tak tentu menghasilkan fungsi yang merupakan antiturunan dari fungsi yang diintegralkan.

Q: Mengapa penting menambahkan konstanta C dalam integral tak tentu?

A: Karena turunan dari konstanta adalah nol, banyak fungsi yang memiliki turunan yang sama. Konstanta C mengakomodasi semua kemungkinan fungsi tersebut.

Q: Bagaimana cara saya memeriksa jawaban integral tak tentu saya?

A: Diferensialkan hasil integral Anda. Jika hasilnya sama dengan fungsi yang diintegralkan, maka jawaban Anda benar.

Semoga contoh soal integral tak tentu di atas membantu Anda memahami konsep integral tak tentu. Prakteklah terus untuk mengasah kemampuan Anda!