Contoh Soal Garis Singgung Persekutuan Luar: Panduan Lengkap

2025-02-13 uncategorized by admin
Contoh Soal Garis Singgung Persekutuan Luar: Panduan Lengkap

Memahami Garis Singgung Persekutuan Luar

Artikel ini akan membahas contoh soal garis singgung persekutuan luar secara detail. Anda akan mempelajari berbagai tipe soal dan bagaimana menyelesaikannya dengan langkah-langkah yang jelas. Setelah membaca artikel ini, Anda akan lebih percaya diri dalam menghadapi soal-soal tentang garis singgung persekutuan luar dalam matematika. Mari kita mulai!

Apa itu Garis Singgung Persekutuan Luar?

Garis singgung persekutuan luar adalah garis lurus yang menyinggung dua lingkaran sekaligus dan terletak di luar kedua lingkaran tersebut. Konsep ini sering muncul dalam soal-soal geometri. Memahami garis singgung persekutuan luar sangat penting untuk menyelesaikan berbagai permasalahan geometri yang melibatkan dua lingkaran.

Rumus Garis Singgung Persekutuan Luar

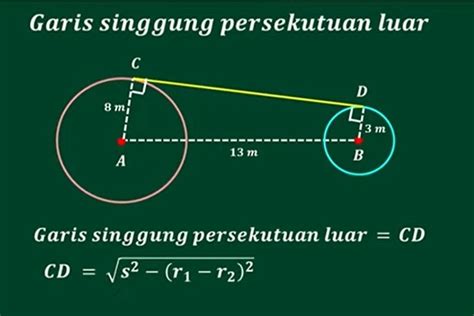
Panjang garis singgung persekutuan luar (d) dua lingkaran dengan jari-jari r₁ dan r₂ serta jarak pusat kedua lingkaran a dapat dihitung menggunakan rumus:

d = √(a² - (r₁ + r₂)²)

di mana:

    1. d = panjang garis singgung persekutuan luar

    2. a = jarak antara pusat kedua lingkaran

    3. r₁ = jari-jari lingkaran pertama

    4. r₂ = jari-jari lingkaran kedua

      5. Rumus ini hanya berlaku jika a > r₁ + r₂. Jika a ≤ r₁ + r₂, maka tidak ada garis singgung persekutuan luar.

      Contoh Soal Garis Singgung Persekutuan Luar dan Penyelesaiannya

      Berikut beberapa contoh soal garis singgung persekutuan luar dengan penyelesaian langkah demi langkah:

      Contoh 1:

      Dua lingkaran memiliki jari-jari 5 cm dan 3 cm. Jarak antara pusat kedua lingkaran adalah 10 cm. Tentukan panjang garis singgung persekutuan luar kedua lingkaran tersebut.

      Penyelesaian:

    5. Identifikasi nilai-nilai yang diketahui: r₁ = 5 cm, r₂ = 3 cm, a = 10 cm.

    6. Gunakan rumus: d = √(a² - (r₁ + r₂)²)

    7. Substitusikan nilai-nilai yang diketahui: d = √(10² - (5 + 3)²) = √(100 - 64) = √36 = 6 cm

    8. Jadi, panjang garis singgung persekutuan luar kedua lingkaran adalah 6 cm.

      9. Contoh 2:

      Dua buah lingkaran masing-masing berjari-jari 4 cm dan 2 cm. Jarak antara kedua pusat lingkaran adalah 8 cm. Berapa panjang garis singgung persekutuan luarnya?

      Penyelesaian:

    9. r₁ = 4 cm, r₂ = 2 cm, a = 8 cm

    10. d = √(8² - (4 + 2)²) = √(64 - 36) = √28 = 2√7 cm

      11. Contoh 3 (Soal yang lebih kompleks):

      Lingkaran A berjari-jari 7 cm dan lingkaran B berjari-jari 3 cm. Jarak antara pusat kedua lingkaran adalah 13 cm. Tentukan panjang garis singgung persekutuan luarnya.

      Penyelesaian:

    11. r₁ = 7 cm, r₂ = 3 cm, a = 13 cm.

    12. d = √(13² - (7 + 3)²) = √(169 - 100) = √69 cm

      13. Tips Mengerjakan Soal Garis Singgung Persekutuan Luar

    13. Pastikan Anda memahami rumus dengan baik.

    14. Identifikasi dengan benar nilai jari-jari masing-masing lingkaran dan jarak antar pusatnya.

    15. Perhatikan satuan yang digunakan.

    16. Lakukan perhitungan dengan teliti.

Tanya Jawab

Q: Apa yang terjadi jika a ≤ r₁ + r₂ dalam rumus garis singgung persekutuan luar?

A: Jika a ≤ r₁ + r₂, maka kedua lingkaran saling berpotongan atau bahkan satu lingkaran berada di dalam lingkaran lainnya. Dalam kasus ini, tidak ada garis singgung persekutuan luar.

Q: Apakah ada perbedaan antara garis singgung persekutuan luar dan dalam?

A: Ya, ada perbedaan. Garis singgung persekutuan luar terletak di luar kedua lingkaran, sedangkan garis singgung persekutuan dalam memotong garis yang menghubungkan kedua pusat lingkaran.

Q: Bagaimana jika saya kesulitan memahami konsep garis singgung persekutuan luar?

A: Cobalah untuk menggambar kedua lingkaran dan garis singgungnya. Visualisasi akan membantu Anda memahami konsep ini lebih baik. Anda juga bisa mencari penjelasan lebih lanjut di buku teks matematika atau sumber belajar online lainnya.

Dengan memahami konsep dan contoh soal garis singgung persekutuan luar di atas, Anda akan lebih siap menghadapi soal-soal yang lebih menantang. Selamat berlatih!

Related Post