Contoh Soal Aturan Cosinus: Mudah Dipahami!
Yuk, kita pelajari aturan cosinus! Aturan cosinus merupakan rumus yang sangat berguna dalam menyelesaikan masalah geometri, khususnya yang berkaitan dengan segitiga. Artikel ini akan memberikan beberapa contoh soal aturan cosinus beserta penyelesaiannya, sehingga Anda bisa langsung mempraktikkannya. Siap? Mari kita mulai!
Memahami Aturan Cosinus
Aturan cosinus menghubungkan panjang sisi-sisi suatu segitiga dengan salah satu sudutnya. Rumusnya adalah:
- a² = b² + c² - 2bc cos A
- b² = a² + c² - 2ac cos B
- c² = a² + b² - 2ab cos C
- a, b, dan c adalah panjang sisi-sisi segitiga.
- A, B, dan C adalah sudut-sudut yang berhadapan dengan sisi a, b, dan c masing-masing.
di mana:
Contoh Soal Aturan Cosinus dan Pembahasannya
Berikut beberapa contoh soal aturan cosinus dengan berbagai tingkat kesulitan:
Contoh 1: Mencari Panjang Sisi
Sebuah segitiga ABC memiliki panjang sisi b = 5 cm, c = 7 cm, dan sudut A = 60°. Tentukan panjang sisi a.
Penyelesaian:
Kita gunakan rumus a² = b² + c² - 2bc cos A
a² = 5² + 7² - 2(5)(7) cos 60°
a² = 25 + 49 - 70 (1/2)
a² = 74 - 35
a² = 39
a = √39 ≈ 6.24 cm
Jadi, panjang sisi a adalah sekitar 6.24 cm.
Contoh 2: Mencari Besar Sudut
Sebuah segitiga PQR memiliki panjang sisi p = 8 cm, q = 10 cm, dan r = 12 cm. Tentukan besar sudut Q.
Penyelesaian:
Kita gunakan rumus q² = p² + r² - 2pr cos Q
10² = 8² + 12² - 2(8)(12) cos Q
100 = 64 + 144 - 192 cos Q
100 = 208 - 192 cos Q
192 cos Q = 108
cos Q = 108/192 = 9/16
Q = arccos (9/16) ≈ 55.77°
Jadi, besar sudut Q adalah sekitar 55.77°.
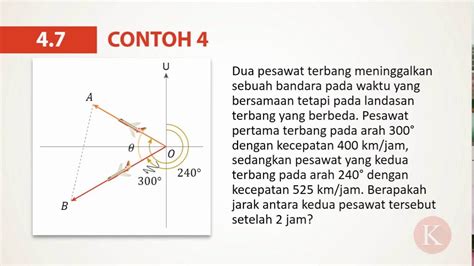
Contoh 3: Soal Cerita
Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 10 km ke arah timur, kemudian berbelok ke arah utara sejauh 8 km menuju pelabuhan C. Tentukan jarak langsung dari pelabuhan A ke pelabuhan C.
Penyelesaian:
Permasalahan ini membentuk segitiga siku-siku. Jarak langsung A ke C dapat dihitung menggunakan teorema Pythagoras, bukan aturan cosinus. Namun, jika sudut belokan bukan 90 derajat, maka kita perlu menggunakan aturan cosinus.
Misalnya, kapal berbelok 75 derajat ke arah utara:
Dalam hal ini, kita memiliki segitiga ABC dengan AB = 10 km, BC = 8 km, dan sudut B = 105° (180° - 75°). Kita ingin mencari AC. Kita gunakan rumus:
AC² = AB² + BC² - 2(AB)(BC)cos(105°)
AC² = 10² + 8² - 2(10)(8)cos(105°)
AC² ≈ 220.47
AC ≈ 14.85 km
Jarak langsung dari pelabuhan A ke pelabuhan C adalah sekitar 14.85 km.
Tanya Jawab Seputar Aturan Cosinus
Q: Kapan kita harus menggunakan aturan cosinus?
A: Gunakan aturan cosinus ketika Anda mengetahui panjang dua sisi segitiga dan sudut di antara keduanya (untuk mencari panjang sisi ketiga), atau ketika Anda mengetahui panjang ketiga sisi segitiga (untuk mencari besar salah satu sudutnya).
Q: Apa perbedaan aturan cosinus dengan aturan sinus?
A: Aturan sinus menghubungkan rasio panjang sisi dengan sinus sudut di hadapannya, sementara aturan cosinus menghubungkan panjang ketiga sisi dengan kosinus salah satu sudutnya. Pemilihan aturan tergantung pada informasi yang diberikan dalam soal.
Q: Apakah aturan cosinus berlaku untuk semua jenis segitiga?
A: Ya, aturan cosinus berlaku untuk semua jenis segitiga, baik segitiga lancip, segitiga siku-siku, maupun segitiga tumpul.
Semoga contoh soal aturan cosinus di atas membantu Anda memahami konsep dan penerapannya. Jangan ragu untuk berlatih lebih banyak soal untuk mengasah kemampuan Anda!